Digital Randomness and AES

2025-05-15 3856 words 19 minutes

Contents

Every time I used a random() function in Python or other programming languages, I found myself wondering how it actually produced a random value, and what it was based on. Today, we’ll dive into that question and break it down.
Since many of these algorithms also play a role in generating cryptographic keys, and I have a university exam coming up on AES and other cryptographic algorithms, this seemed like the perfect opportunity to connect the dots between the two topics.

This post will be divided into two parts: first, we’ll discuss digital randomness, and then we’ll dive into one of the most used encryption algorithm: AES.

Digital Randomness

Randomness in computing is typically produced by pseudorandom number generators (PRNGs) algorithms that deterministically generate sequences of numbers that appear random. True physical randomness is rare in digital devices (which are deterministic), so operating systems and software rely on PRNGs seeded with small unpredictable inputs (entropy) to produce random outputs.
We can define two classes of PRNG:

General-purpose PRNGs: are designed for speed and statistical uniformity scopes, sacrifice security and are used like in the Python’s random module.
Cryptographically secure PRNGs (CSPRNGs): designed for unpredictability and security, ensure outputs cannot be predicted even with partial knowledge of their internal state, and are usually used for cryptographic keys, token etc.

General-Purpose Number Generators (PRNGs)

General-purpose PRNGs are deterministic algorithms initialized with a seed. They produce sequences of numbers that have properties of uniform randomness for statistical purposes. As we said before, these algorithms are fast and have very long repeat cycles (periods), but are not cryptographically secure, given enough outputs or the internal state, an attacker could predict future outputs.
Two of the most widely used general-purpose PRNG algorithms that we’re going to see in detail are the Linear Congruential Generator (LCG) and the Mersenne Twister.

Linear Congruential Generator (LCG)

LCGs are among the oldest and simplest PRNGs. An LCG produces a sequence of values using a linear recurrence formula:
$X_{n+1} = (a \cdot X_n + c)$ mod $m$
where $X_n$ is the current number, $a$ multiplier, $c$ increment value and $m$ modulus that define the generator. With good choose of parameters they can have quite long period, for example:

C libraries (e.g. rand()): modulus $m = 2^{31}$, $a$ = 1103515245 and $c$ = 12345
Apple CarbonLib: modulus $m=2^{31}-1$, $a$=16807 and $c$ = 0

LCGs are easy to implement and very fast, given the linear nature, but due to this nature they have also critical weaknesses, giving an predictable (invertible) output sequence, and more in general the quality of the output is highly sensitive to the choice of parameters: poor parameter choose lead to short periods and easily predictable patterns. Following the golden rule of cryptography, that using well-established, thoroughly tested solutions is always better than creating your own; we can say that using well-studied parameters is definitely preferred.

Marsenne Twister - MT 19937

The Mersenne Twister is one of the most widely used pseudorandom number generators (PRNGs) due to its speed and statistical properties. It was designed to produce high-quality pseudorandom numbers with an extremely long period of $2^{19937}-1$, making it suitable for multiple non-cryptographic applications, like simulations or modeling. This algorithm is the default in many programming environments, including the random() module in Python.

The Mersenne Twister maintains an internal state made up of an array of 624 32-bit integers. Each time a number is generated, this internal state is updated to produce a new pseudorandom value. The generation process involves several key steps:

The state array is initialized using a seed, which can be provided by the user or derived from an entropy source such as the system time.
The state is then transformed through a series of bitwise operations, logical shifts, and modular arithmetic.
A crucial “twist” step mixes bits across adjacent elements in the array, helping to achieve a long period and reduce linear correlations.
New values are generated by applying bitmasks and performing left and right shifts, which further scramble the bits.
The final output is then tempered, using a sequence of XOR and shift operations to improve the uniformity and statistical quality of the output.

Despite its efficiency, this algorithm is completely unsuitable for cryptographic applications. Its main weakness lies in its deterministic nature: if an attacker obtains 624 consecutive output values, they can reconstruct the internal state of the generator. Once this state is known, all future outputs can be predicted with high accuracy. Additionally, if the seed used to initialize the generator is known or can be guessed, the entire sequence of outputs can be replicated.

Cryptographically Secure PRNGs (CSPRNGs)

A pool is a data structure that accumulates entropy collected from various sources, such as hardware events, user input timing, disk activity, or network traffic. This collected entropy represents unpredictable, high-quality randomness. The pool acts as a buffer, storing entropy until it reaches a sufficient threshold, at which point it can be used to seed or reseed a cryptographically secure pseudorandom number generator (CSPRNG). Entropy pools are vital for ensuring that random output remains secure, especially in environments where randomness must resist analysis or prediction by attackers.

CSPRNGs are algorithms designed to produce random sequences that are unpredictable and robust against attackers. Even if an attacker knows the algorithm and has seen outputs, they should not be able to feasibly determine the internal state or predict future outputs. Unlike general PRNGs which might be seeded once and then run indefinitely, CSPRNGs are often periodically “reseeded” with fresh entropy to protect them against state compromise, and they employ cryptographic primitives (like hash functions) to mix entropy and generate output. In practice, operating system CSPRNGs continually accumulate entropy from various sources and use algorithms like those described below to produce secure random bytes on demand.

Fortuna Algorithm

Fortuna is a CSPRNG designed to improve its predecessor Yarrow. It introduce more sophisticated entropy management strategy and a secure generator mechanism based on modern cryptographic primitives.
An interesting key of Fortuna is the use of 32 independent entropy pool, that are not used equally in reseeding the generator. Pool 0 is used in every reseed, while higher-numbered pools are reseed less frequently, like, pool k contributes to every $2^{k-th}$ reseed. For example, pool 1 is used every second reseed, pool 2 every fourth, and so on.
This exponentially increasingly contribution model ensures that older pools accumulate more entropy before being used, adding depth and resilience to the entropy collection process.

Even if some entropy sources are observable or manipulable by an attacker, as long as at least one pool eventually gathers unpredictable input, the generator can be reseeded securely. The design also prevents adversaries from triggering frequent reseeds to deplete the entropy, thanks to the progressive integration schedule of the pools.

One of Fortuna’s strengths is its reseeding mechanism. After generating a certain amount of output, the system reseeds the generator key with fresh entropy. Even if no new entropy is available, periodic reseeding still occurs to enforce forward secrecy. This key erasure process, make sure that if the internal state is ever compromised, past outputs remain secure because previous keys are overwritten and cannot be recovered. The cryptographic security of Fortuna’s output is directly tied to the underlying cipher. With AES, the output is identical from true randomness if the key is unknown. Furthermore, once the generator is reseeded, any prior compromise becomes irrelevant: the new key severs any link between past and future output sequences.

NIST DRBGs (AES-CTR DRBG)

Another important category of CSPRNGs comes from a NIST publication which specifies several Deterministic Random Bit Generators for cryptographic use.
One largely adopted DRBG from this suite is AES-CTR DRBG, which uses the Advanced Encryption Standard (AES) in counter mode (CTR) as its core mechanism. We’ll discuss more deeply on AES and different operating modes in the next part. The internal state of this generator consists of two main components: a secret AES key and a value known as ‘V’, which acts as a nonce.
To generate random output, the generator repeatedly encrypts the current value of V with the key, producing blocks of pseudorandom bits. After each encryption, V is incremented, ensuring that each input to AES is unique.

To maintain security over time, the generator periodically reseeds itself. This reseeding process injects new entropy into the internal state, either by rekeying AES entirely or by adding new entropy into the existing state using a defined update function (e.g., XOR transformations).
OpenSSL has historically used AES-CTR DRBG as its default random number generator in FIPS-compliant builds. It’s also used in trusted platform modules (TPMs) and secure hardware enclaves where deterministic yet cryptographically sound randomness is needed.

An important note to make is that not all standard DRBGs have the same reputation: there was a controversy with the Dual_EC_DRBG (Dual Elliptic Curve) from the same NIST suite due to a suspected NSA backdoor (which is a bit creepy btw).

ChaCha20

ChaCha20 is a modern stream cipher that became popular for CSPRNGs due to its blend of high performance, simplicity, and robust security properties, especially on general-purpose CPUs lacking AES-specific hardware acceleration.

It operates with a 256-bit key and a 64-bit nonce, producing a pseudorandom keystream by applying a permutation-based function, named ChaCha core, for 20 rounds. Each iteration produces a 64-byte block, and up to $2^{64}$ such blocks can be generated for a given key and nonce pair. The cipher’s design ensures that the output appears indistinguishable from true randomness when the key is secret, and it has proven resistant to cryptanalysis over the years.

Major operating systems and crypto libraries, including Linux’s /dev/urandom, OpenBSD’s arc4random, and BoringSSL, now use ChaCha20-based constructions for secure random number generation. Another interesting fact is that many modern ransomware adopted ChaCha20 as their encryption algorithm due to its efficiency of encrypting large files without relying on hardware specific feature, making it perfects for deploying across wide range of systems.

Entropy Sources and OS Entropy Pools

What makes a CSPRNG secure is not just the algorithm, but also how it’s seeded and reseeded with ’true’ randomness. If a CSPRNG is initialized with insufficient entropy, its outputs could be guessed.
Weak PRNGs can enable cross-layer attacks where predictability in random number generation at one layer compromises security at another. Researchers have demonstrated howi such attacks can affect UDP at the network level, highlighting the risks of weak entropy.

Thus, above algorithms rely on an entropy source to provide an initial seed and occasional refresh. The operating system’s role is crucial here: it must collect noise from hardware events, user input, or dedicated hardware random generators to feed the CSPRNG.

Modern CPUs also often provide instructions like Intel’s RDRAND or RDSEED, which leverage on-chip hardware random number generators (usually built from analog circuits) to provide entropy. Dedicated hardware RNGs (like those in TPMs) can also feed entropy. Even things like differences in CPU instruction timing, due to random cache collisions or branch mispredictions can be used as entropy sources in some systems.

Operating systems typically funnel all these unpredictable events into an entropy pool that we mentioned before. Each event (e.g mouse moved at time X with coordinates Y) is not purely random, but might contribute a few bits of unpredictability. The OS uses a mixing function (usually hash functions) to combine this new data into the pool in a one-way manner. The goal is that the pool’s contents evolve in a pseudo-random way that accumulates all the entropy that has been added. Ideally, an attacker shouldn’t be able to figure out the pool contents even if they see the incoming events (because they’re hashed/mixed together in a secret state).

The entropy pool design means that even if an application requests a large number of random bytes, the system doesn’t literally consume that many bits of raw entropy; instead it uses the pool as a seed to a generator (like ChaCha20 or AES-CTR). This is crucial for performance: true entropy might be collected at a slow rate, but applications might need thousands of random bits per second. The PRNG acts as an entropy expander. As long as the internal state has for example 256 bits of true entropy, it can generate many megabytes of output that are computationally infeasible to predict without knowing the state, thanks to the cryptographic whitening.

When random bytes are requested from the OS, they are produced by whitening the entropy pool, typically, running a cryptographic function on the pool or on a subset of the pool. Classic unix-like systems had two main interfaces: /dev/random and /dev/urandom.

AES - Advanced Encryption Standard

In the first part we discussed on digital randomness and entropy, and we saw how crucial truly random values are to cryptographic security. Symmetric encryption algorithms like the Advanced Encryption Standard (AES) rely on this principles; a strong algorithm is only as secure as the randomness of its keys and nonces. If AES keys are generated with too little entropy, their predictability can weaken the overall security of the cipher.

AES is a symmetric block cipher algorithm designed to replace the older DES algorithm. It operates on fixed-size blocks of 128 bits and supports key sizes of 128 (AES-128), 192 (AES-192), or 256 bits (AES-256). The block cipher’s structure is a substitution–permutation network, meaning AES achieves encryption through repeated layers of substitution (non-linear transformations) and permutation (mixing of bits for diffusion). Depending on the key length, the algorithm executes a sequence of rounds: 10 rounds for 128-bit keys, and 14 rounds for 256-bit keys. Each round applies a fixed set of operations that we are about to see, to transform the data, so that the output ciphertext appears essentially random for anyone without the key.

How does AES Works

Before encryption begins, the 128-bit plaintext is loaded into a 4×4 byte matrix called the state. AES starts with an initial AddRoundKey step (often called the initial key whitening), where the state is combined with the initial cipher key, by bitwise XOR. After this, the state undergoes a series of rounds. Each round (except the final round) consists of four transformations applied in sequence:

SubBytes: a non-linear substitution step where each byte in the state is replaced with a corresponding byte from a fixed 8-bit substitution box (S-box). This provides non-linearity: every byte is transformed independently according to an invertible lookup table . The AES S-box (derived from the multiplicative inverses in GF($2^8$) combined with an affine transform) is designed to have no fixed points and to resist known cryptanalysis attacks. The goal of this step is to confuse the relationship between the plaintext and ciphertext bytes.
ShiftRows: a permutation step that cyclically shifts the bytes in each row of the state matrix by a certain offset. The first row remains unshifted, the second row is rotated left by 1 byte, the third row by 2 bytes, and the fourth row by 3 bytes. This simple row rotation moves bytes to different columns, ensuring that columns are not treated independently after this step. This phase contributes to diffusion by spreading the influence of each byte over multiple columns.
MixColumns: a linear mixing operation that operates on each column of the state. Each column (4 bytes) is transformed by a fixed invertible linear function (multiplication by a constant matrix in GF($2^8$)). As result, the four bytes of a column are mixed together to produce new values for that column MixColumns causes each input byte to affect all four output bytes of its column, providing inter-byte diffusion. After MixColumns, each byte of the state is a linear combination of bytes from the previous round, which helps dissipate patterns and correlations.
AddRoundKey: each byte of the state is XORed with the corresponding byte of the round subkey. This is the only step that directly injects key data into the state, and it effectively encrypts (or decrypts) the data with the subkey. XOR is its own inverse, which is why the same process (with round keys applied in reverse order) is used for decryption. The round key ensures that the transformations of each round depend on the secret key, and without the correct key, an attacker cannot reverse the substitutions and permutations performed.

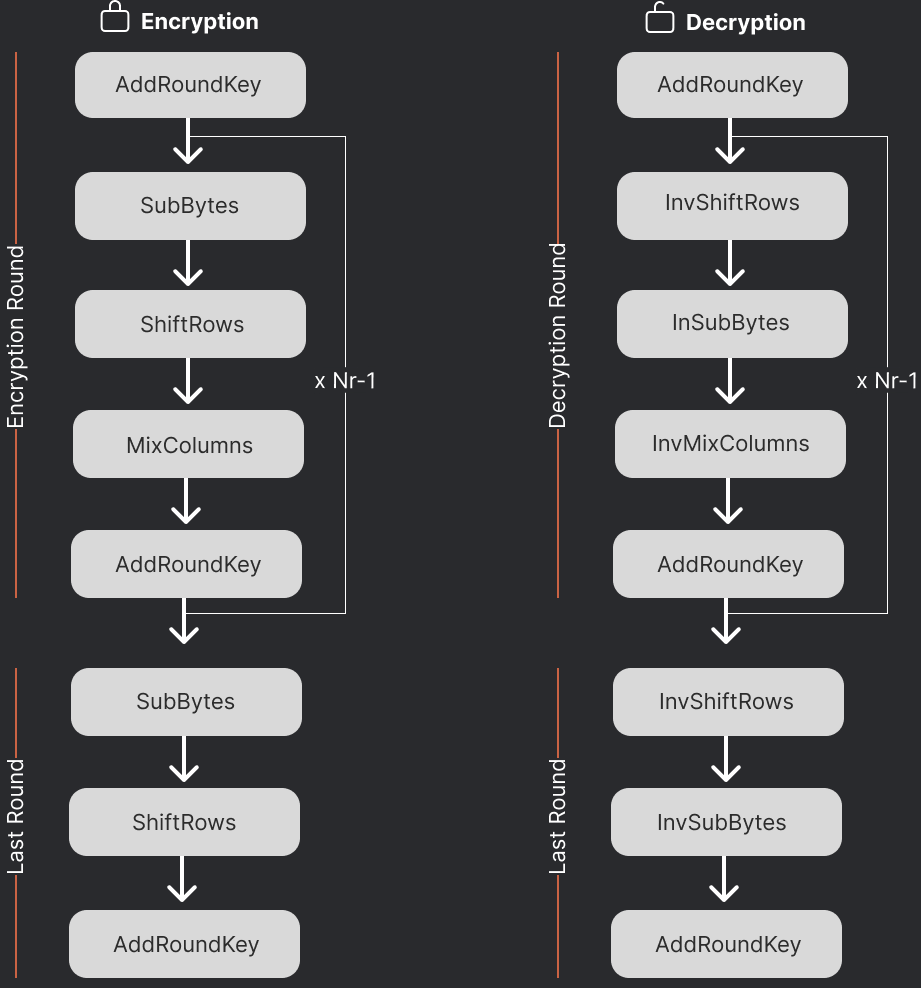
By the last round, the ciphertext appears indistinguishable from random noise for someone lacking the key. Note that the final round of AES skips the MixColumns step, performing only SubBytes, ShiftRows, and AddRoundKey. This is done because MixColumns is linear and its inverse can be combined with the next round’s key addition; leaving it out in the last round ensures symmetry between encryption and decryption processes while still maintaining security. A tiny change in the input will, after a few rounds, completely alter the state in an unpredictable way (avalanche effect).

Modes of Operation

On its own, AES (like any block cipher) encrypts only a fixed-size block of 128 bits. However, real-world data is usually much larger or may not align exactly to a prefixed size block. Modes of operation are standardized techniques to use a block cipher like AES on arbitrary-length data securely. A mode of operation defines how to repeatedly apply the cipher and how each block’s encryption/decryption should depend on others.
We will examine the major AES modes: ECB, CBC, CFB, OFB, and CTR, explaining how each works.

Electronic Codebook (ECB)
This is the simplest AES mode. In ECB mode, the message is divided into 128-bit blocks, and each block is encrypted entirely independently using the AES cipher and the key. There is no additional input besides the plaintext block and the key.
ECB deterministically maps identical plaintext blocks to identical ciphertext blocks (under the same key). As a result, ECB fails to hide data patterns, since it provides no diffusion across blocks. If an attacker knows or can guess parts of the plaintext, they might recognize those patterns in the ciphertext. The only pros of ECB are its simplicity and parallelism: since each block is independent, errors in one block do not affect others, and blocks can be encrypted or decrypted in any order.
Cipher Block Chaining (CBC)
Each plaintext block is XORed with the previous ciphertext block before being encrypted with AES, meaning that each ciphertext block depends on all plaintext blocks up to that point. The initialization vector (IV) is a random 128-bit block that starts the chain for the first block. Because each plaintext is mixed with the previous ciphertext, identical plaintext blocks no longer encrypt to identical ciphertext unless they occur at the same position and after identical history, which is unlikely. This destroys the raw patterns that was letting ECB vulnerable. That being said, the main weakness is that the dependence between blocks means encryption in CBC cannot be parallelized: each plaintext block’s encryption must wait for the previous block’s ciphertext.
Cipher Feedback (CFB)
This mode is essentially a way to turn a block cipher into a self-synchronizing stream cipher. It introduces feedback like CBC, but instead of XORing plaintext with the previous ciphertext before encryption, CFB encrypts the previous ciphertext (or IV for the first block) first, and then XOR that encryption output with the current plaintext block to produce the ciphertext. Decryption uses the same mechanism in reverse, but we still encrypt the previous ciphertext with AES, then XOR with the current ciphertext to recover plaintext. This is why CFB is called self-synchronizing, because if a bit is lost or added in the ciphertext stream, the decryption will gradually re-synchronize after processing a certain number of bits.
Like CBC, also requires an IV for the first block and cannot be parallelized on encryption and like any stream cipher is vulnerable if bits of keystream are ever reused, never reuse an IV with the same key. Also, like CBC, CFB does not provide authenticity, and certain modification or bit-flipping attacks are possible if used without a separate authentication layer.
Output Feedback (OFB)
This mode generates keystream blocks independently of the plaintext or ciphertext; it repeatedly encrypts the evolving state to produce a sequence of pseudorandom outputs, which are then XORed with the plaintext to get ciphertext. It is a synchronous stream cipher mode (as opposed to CFB’s self-synchronizing property). This means if a bit is lost or added in transmission, the sender, and receiver’s keystreams will fall out of sync and decryption will produce unreadable output from that point on. On the other hand, OFB has the property that errors do not propagate: if a single ciphertext bit is flipped in transit, only the corresponding plaintext bit will be corrupted upon decryption, and the rest of the plaintext remains intact.
Counter (CTR)
CTR mode is one of the most popular modes for modern applications. Like OFB, CTR mode transforms a block cipher into a stream cipher by generating a keystream that is XORed with the plaintext. However, instead of using feedback or repeatedly encrypting the previous output, CTR mode generates the keystream by encrypting a counter value that changes with each block. A simple way to implement CTR is to have a counter (unique value) that starts at some nonce and increments by 1 for each following block. The crucial security requirement is that no counter value is ever reused with the same key, across all messages.
The strengths of this mode is that it’s parallelizable, so different blocks can be processed independently of each other. Because the keystream can be generated for any given counter value, you can encrypt/decrypt blocks out of order. For example, if you’re encrypting a large file or data stream and want to access the middle, CTR allows you to do that.

Real-World Applications

AES it’s not just an academic algorithm, it’s crucial in the security of web communications. The HTTPS protocol (TLS/SSL), often uses AES, typically in modes like GCM or CBC, to encrypt HTTP traffic.

AES is also crucial in Wi-Fi security: the WPA2 and WPA3 protocols used in wireless networks rely on AES encryption to protect data.
Some end-to-end encrypted apps use derivatives of AES. For example, WhatsApp employs the Signal Protocol, which utilizes AES-256 in CBC mode to encrypt message payloads after a Diffie-Hellman key exchange.
Password managers such as LastPass and ProtonPass also use AES-256 to encrypt vault data.

Many VPN protocols rely on AES for secure data tunneling. Recently, some YouTubers have begun promoting the same old VPN services with a new selling point: claiming they now support some form of anti-quantum encryption. The idea is that this will prevent future malicious actors from decrypting and viewing your past activity once quantum computers become available.
On that note, I came across an interesting paper which found that AES remains a relevant and secure option in a post-quantum context, provided appropriate key sizes are used. The research also demonstrates how high-speed AES implementations can be integrated into post-quantum key encapsulation mechanisms.
In summary, AES it’s still crucial for modern applications and it seems it will remain crucial also in the future.

This post turned out longer than expected but I learned a ton of new things. Hope it was fun to read too :)