Data Privacy: k-anonymity, differential privacy and more

2024-12-01 2597 words 13 minutes

Contents

In this post we’re going to talk about four data anonymization techniques and we’ll see some related python scripts. Data anonymization allows to protect sensitive information while maintaining the usefulness of datasets for analysis and testing.

K-anonymity

The core of k-anonymity principle states that for any combination of quasi-identifiers (attributes like zip code, birth date, gender, or ethnicity), each record must be indistinguishable from at least k-1 other records. In other words, we can say that k-anonymity protects the privacy of individual persons by pooling their attributes into groups of at least k-1 people.

K-anonymity achieves its privacy goal through two main tools:

suppression: by removing or redacting certain values
generalization: by reducing the precision or granularity of data, such as replacing a specific age with an age range or just the first three digit of a postal code instead of the full one.

Finding the perfect balance in data anonymization is one of the most challenging aspects of privacy-preserving data publishing. The “ideal” level of anonymization isn’t a one-size-fits-all solution and it’s deeply dependent on the intended use case of your data. Let’s consider a medical research dataset: if we over-anonymize by aggressively grouping age ranges or removing too many demographic details, researchers might miss crucial patterns in disease progression across different age groups or populations. However, if we try to preserve too much detail, we risk exposing sensitive patient information. For instance, even seemingly innocuous combinations of zip code, age, and gender can sometimes be enough to re-identify individuals when cross-referenced with public records (background knowledge).

The key lies in understanding your data’s purpose and its sensitivity level: a dataset used for broad statistical analysis might tolerate more aggressive anonymization than one used for machine learning model training, where subtle patterns in the data could be critical. This might mean implementing different levels of anonymization for different use cases, or creating multiple versions of the same dataset with varying degrees of privacy protection.

Talking about optimal generalization, let Ti and Tj be two table such that Tj is the processed one (Ti<=Tj), we can say that this new table is a k-minimal generalization of the initial table if it meets the following three criteria:

There is not another table with the same distance vector that allows me to meet minimal suppression criteria: essentially, we’re not over-suppressing data when we don’t need to.
The difference in size between our original table (Ti) and the generalized table (Tj) can’t exceed our maximum suppression threshold set by the user (called maxSUP).
If we have any other table that satisfies the first two conditions, its domain values shouldn’t be more specific than our generalized table. This means we’ve found the sweet spot where we’re generalizing just enough to achieve k-anonymity, but not more than necessary.

As we said before, when it comes to choosing the best way to generalize our data, we have several approaches to consider depending on the balancing between data utility and privacy:

Minimum absolute distance: it is like taking the shortest path to anonymization. It simply counts the total number of generalization steps we take, regardless of which attributes we’re generalizing. For example, whether we’re grouping ages into ranges or combining zip codes, we just want the fewest total changes.
Minimum relative distance: it takes into account that some attributes have more levels of generalization than others. Imagine generalizing a 5-digit zip code versus a binary gender field; each step in the zip code hierarchy might be considered less impactful since there are more possible steps. It’s like normalizing our changes across different scales.
Maximum distribution: it is all about maintaining data diversity. This approach favours generalizations that keep as many distinct combinations of values as possible. It’s particularly useful when you need to preserve the variety in your dataset for meaningful analysis.
Minimum suppression: it focuses on keeping as many records as possible. Rather than removing records that don’t fit neatly into our anonymization scheme, this approach tries to find generalizations that let us keep more of our original data points. It’s like trying to minimize the number of records we have to throw away, to achieve privacy.

k-loose

To further increase data anonymity we can introduce the k-loose algorithm. This algorithm introduces data fragmentation by splitting the table and linking not the single rows, but groups of rows, thereby adding an extra layer of protection.

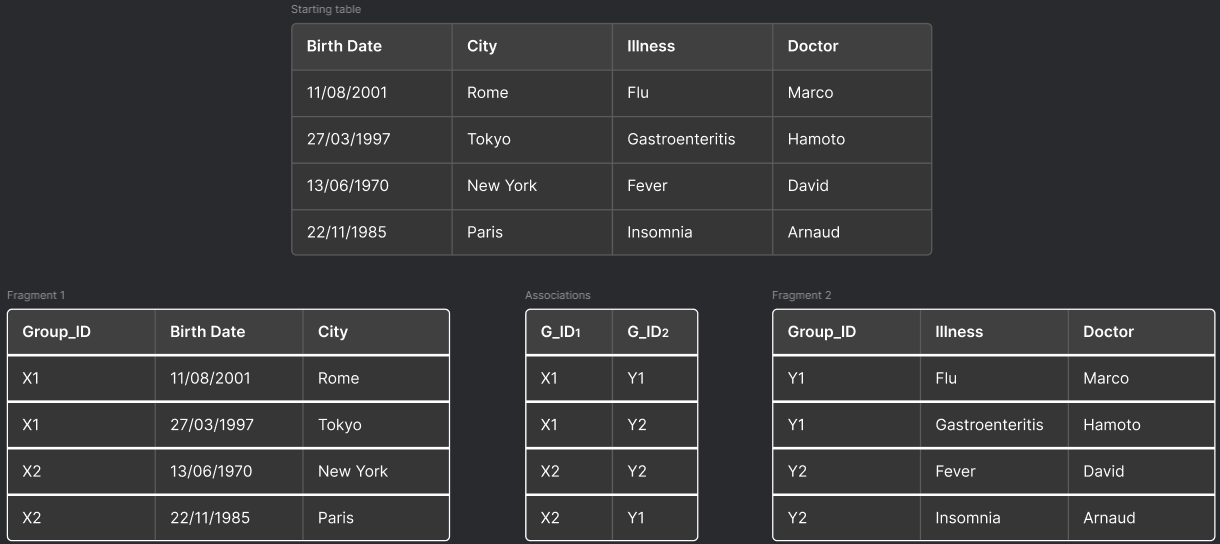
k is calculated as the product of two groups, which can be done in two ways:

Flat grouping: This occurs when one of the two groups equals one (e.g., to achieve k=12, we have k1=1 and k2=12).
Sparse grouping: This occurs when neither of the two groups equals one.

The criteria for splitting can be based on confidentiality constraints that the data provider must adhere to, while also considering visibility constraints to maintain the usefulness of the data.

By linking groups of rows rather than individual entries, k-loose significantly reduces the risk of unauthorized data reconstruction. Even if an attacker gains access to multiple fragments, the ambiguity introduced by group associations makes it extremely challenging to piece together the original dataset.

Python Script

This example script achieve k-anonymity starting from a dataset containing ‘Name’, ‘Age’, ‘ZIP’ and ‘Salary’ fields. We defined k = 3 and that means that each unique combination of quasi-identifiers must appear in at least three records in the dataset.

data = { 
	'Name': ['Alice', 'Bob', 'Charlie', 'David', 'Eve', 'Frank', 'Grace', 'Heidi', 'Ivan', 'Judy'], 
	'Age': [23, 24, 45, 52, 23, 54, 23, 34, 45, 52], 
	'ZIP': [12345, 12345, 54321, 54321, 12345, 54321, 12345, 23456, 54321, 54321], 'Salary': [70000, 80000, 50000, 55000, 72000, 57000, 71000, 69000, 51000, 53000]
} 
df = pd.DataFrame(data)

k = 3

To reach the k-anonymity we decide to suppress one identifying information by removing the name column and generalizing the age into age ranges and the zip code by removing the last digit to reduce specificity:

df = df.drop(columns=['Name'])

def generalize_age(age):
    if age %3C 30:
        return '20-29'
    elif age < 40:
        return '30-39'
    elif age < 50:
        return '40-49'
    else:
        return '50-59'

df['Age'] = df['Age'].apply(generalize_age)

def generalize_zip(zip_code): return str(zip_code)[:4] + '*' df['ZIP'] = df['ZIP'].apply(generalize_zip)

Finally we check if we met the ‘k’ requirement by grouping the records that have the same values and counts the number of records in each group:

def is_k_anonymous(df, k):
    grouped = df.groupby(['Age', 'ZIP', 'Salary']).size()
    return all(count %3E= k for count in grouped)

if is_k_anonymous(df, k):
    print("The dataset meets k-anonymity.")
else:
    print("The dataset does not meet k-anonymity and may require further generalization or suppression.")

l-diversity

To explain the next two methods we need to introduce the concept of a “q-block” which is a set of records sharing the same values for all quasi-identifier attributes in a dataset. We can think of it as a group of records that look identical when considering only the attributes that could potentially identify someone. l-diversity addresses a critical weakness in k-anonymity by focusing on the diversity of sensitive values within each q-block. While k-anonymity ensures that individuals can’t be uniquely identified, it doesn’t protect against attribute disclosure when sensitive values in a q-block are too homogeneous.

l-diversity requires that each q-block must contain at least ‘l’ “well-represented” different values for sensitive attributes. For example, if we have a medical dataset where diagnosis is the sensitive attribute, l-diversity with l=3 would require each q-block to have at least three different diagnoses.

However, as you can image, l-diversity also has its limitations:

skewness attack: l-diversity does not consider the overall distribution of sensitive values in the dataset. Imagine a dataset where 90% of individuals have a “common cold” diagnosis, while 10% have “cancer”. A q-block satisfying 2-diversity might have these exact same proportions, technically diverse, but an attacker could still confidently guess that any individual in that q-block likely has a common cold. This skewed distribution means that even with l-diversity satisfied, the probability inference of sensitive values remains possible because the attacker can leverage knowledge of the overall data distribution to make accurate predictions about individuals in specific q-blocks.
similarity attack: l-diversity doesn’t consider the semantic closeness of sensitive values, for example: if all diseases in a q-block are different but related (like various types of cancer), the protection might still be insufficient. An attacker might not know the exact condition, but they can still know that the individual has a cancer-related illness. This semantic similarity among supposedly different values does not allow the privacy that l-diversity aims to provide.

Python Script

Similar to the k-anonymity code we can define a sample dataset with some personal information and diagnosis:

data = { 
	'Name': ['Alice', 'Bob', 'Charlie', 'David', 'Eve', 'Frank', 'Grace', 'Heidi', 'Ivan', 'Judy'], 
	'Age': [23, 24, 45, 52, 23, 54, 23, 34, 45, 52], 
	'ZIP': [12345, 12345, 54321, 54321, 12345, 54321, 12345, 23456, 54321, 54321], 
	'Diagnosis': ['Flu', 'Cold', 'Flu', 'Diabetes', 'Cold', 'Flu', 'Cold', 'Diabetes', 'Diabetes', 'Flu'] 
} 

df = pd.DataFrame(data)

We can then define our quasi-identifiers, sensitive attribute and set the desired level of l-diversity. In this example we used a l=2:

quasi_identifiers = ['Age', 'ZIP'] 
sensitive_attribute = 'Diagnosis' 

l = 2

Then we can group by quasi-identifier (q-blocks), define a function that checks for l-diversity in each block by counting unique values within each q-block and then we call it:

grouped = df.groupby(quasi_identifiers)

def check_l_diversity(group, sensitive_attr, l):
    unique_values = group[sensitive_attr].nunique()
    return unique_values %3E= l

l_diverse = grouped.apply(lambda group: check_l_diversity(group, sensitive_attribute, l))

if l_diverse.all(): 
	print("The dataset satisfies l-diversity.") 
else: 
	print("The dataset does NOT satisfy l-diversity.")

t-closeness

t-closeness represents another privacy model that builds upon the foundations of k-anonymity and l-diversity by focusing on the distribution of sensitive values within each q-block. The principle behind this method is that the distribution of sensitive values within any q-block should be close to their distribution in the overall dataset, with ’t’ representing the maximum allowed difference between these distributions. In other words, the distance between the distribution of a sensitive attribute in any q-block and the distribution of the same attribute in the whole dataset should not exceed a threshold t.

For example, if in our medical dataset, 15% of patients have diabetes, 10% have hypertension, and 5% have arthritis, then each q-block should maintain a similar distribution, with the difference not exceeding t. This closeness is typically measured using Earth Mover’s Distance (EMD), which calculates how much work is needed to transform one distribution into another. The EMD takes into account not just the frequency of values but also how semantically different they are from each other, meaning it understands that the difference between salaries of $20K and $30K is smaller than the difference between $20K and $80K. So EMD would measure how much “work” is needed to transform the q-block’s distribution to match the global distribution.

Python Script

In the following example we will apply t-closeness to a dataset of medical records and we will use a threshold of 0.2 which will be the maximum allowed distance between distributions.

class TCloseness: 
	def __init__(self, threshold=0.2): 
	self.threshold = threshold 
	self.global_distribution = None

We need to define a function to calculate EMD between two distributions, normalizing them and calculating the Wasserstein distance (1D EMD):

	def _calculate_emd(self, dist1, dist2, ordered_values): 
		p1 = np.array([dist1.get(val, 0) for val in ordered_values]) 
		p2 = np.array([dist2.get(val, 0) for val in ordered_values]) 
		p1 = p1 / p1.sum() if p1.sum() > 0 else p1 
		p2 = p2 / p2.sum() if p2.sum() > 0 else p2 
		return wasserstein_distance(np.arange(len(ordered_values)),
		 np.arange(len(ordered_values)), p1, p2)

We can now calculate distribution of values in a series and check if the example dataset satisfies t-closeness:

	def _get_distribution(self, data): 
		return Counter(data) 
		
	def check_t_closeness(self, df, quasi_identifiers, sensitive_attribute): 
		self.global_distribution = self._get_distribution(df[sensitive_attribute]) 
		ordered_values = sorted(self.global_distribution.keys()) 
		grouped = df.groupby(quasi_identifiers) 
		violations = {} 
		satisfies_t_closeness = True 
	
	for group_name, group in grouped: 
		local_distribution = self._get_distribution(group[sensitive_attribute]) 
		distance = self._calculate_emd(local_distribution, self.global_distribution, ordered_values) 
		
		if distance > self.threshold: 
			satisfies_t_closeness = False 
			violations[group_name] = { 
			'distance': distance, 
			'local_distribution': dict(local_distribution), 
			'records_count': len(group) } 
	return satisfies_t_closeness, violations

A main ‘anonymize_medical_records’ function that through iterative basic generalization for quasi-identifiers allows to achieve our t-closeness desired level:

def anonymize_medical_records(df, quasi_identifiers, sensitive_attribute, t_threshold=0.2): 
	df_anonymized = df.copy() 
	t_closeness = TCloseness(threshold=t_threshold) 
	satisfies, violations = t_closeness.check_t_closeness(df_anonymized, quasi_identifiers, sensitive_attribute) 
	
	if not satisfies: 
		for qi in quasi_identifiers: 
			if df_anonymized[qi].dtype in [np.int64, np.float64]: 
			df_anonymized[qi] = pd.qcut(df_anonymized[qi], q=5, labels=False, duplicates='drop') 
			else: 
			df_anonymized[qi] = df_anonymized[qi].astype('category').cat.codes 
	return df_anonymized 
	
if __name__ == "__main__": 
	data = { 'age': np.random.randint(20, 80, 1000), 
	'zipcode': np.random.randint(10000, 99999, 1000), 
	'gender': np.random.choice(['M', 'F'], 1000), 
	'disease': np.random.choice( 
		['Flu', 'Diabetes', 'Heart Disease', 'Hypertension', 'Arthritis'], 
		1000, 
		p=[0.3, 0.2, 0.2, 0.15, 0.15] ) } 


df = pd.DataFrame(data) 
quasi_identifiers = ['age', 'zipcode', 'gender'] 
sensitive_attribute = 'disease' 

df_anonymized = anonymize_medical_records(df, quasi_identifiers, sensitive_attribute, t_threshold=0.2) 

t_closeness = TCloseness(threshold=0.2) 

satisfies, violations = t_closeness.check_t_closeness(df_anonymized, quasi_identifiers, sensitive_attribute) 

print(f"Dataset satisfies t-closeness: {satisfies}")

Differential Privacy

Although k-anonymity, combined with the other methods seen before, can protect against certain forms of re-identification, it has its limitations, particularly in scenarios where attackers possess prior knowledge about the data. To address this, we can implement differential privacy, a framework that fundamentally incorporates a controlled level of noise or randomness into the data or query results, calibrating them to maintain the utility of the data. Unlike k-anonymity, which depends on structural or lexical transformations, differential privacy takes a semantic approach.

The key principle of differential privacy is the privacy budget (denoted as ε), which quantifies the maximum information leakage allowed during data analysis. A lower ε value indicates stronger privacy guarantees, but at the cost of reduced data utility. This trade-off is fundamental to the approach: as more noise is introduced, individual record details become increasingly obscured, but the statistical properties of the aggregate data remain meaningful. The noise can be applied to the query results (global approach) or directly to individual data points before they are shared (local approach).

Another mathematical factor involves computing the sensitivity of a query (denoted as Δ), essentially how much a single record could potentially change the query’s output. This sensitivity becomes the basis for calibrating the noise addition. By mathematically bounding the probability distribution of query results with and without a specific record.

The two most common mechanisms for implementing differential privacy are:

Laplace Mechanism: Adds noise drawn from the Laplace distribution to query results, often used for numerical data. Noise is drawn from a Laplace distribution, which is shaped like a double-sided exponential curve centered at zero. This distribution is symmetric, meaning it is equally likely to add positive or negative noise to the result. As we said before, the amount of noise added is determined both by privacy budget and sensitivity. The noise magnitude is proportional to the ratio Δ/ϵ ensuring that queries with higher sensitivity or stricter privacy requirements have more noise added.
Exponential Mechanism: Usually used with non-numerical data, perturbs categorical outputs by selecting results based on their utility scores, weighted by a probability distribution. Instead of adding noise directly to the result, it modifies the selection process to favour certain outcomes probabilistically. This method is usually also more computationally intensive then the previous one.

Examples of real time usage can be seen in healthcare and medical research, where for example genomic research uses large-scale genomic studies require sharing vast amounts of sensitive genetic data. Differential privacy allows researchers to perform aggregate statistical analyses while preventing re-identification of individual genetic profiles. Same thing for a hospital Performance Tracking program, where we can analyse treatment outcomes, complication rates, and patient demographics without exposing individual records.

Another practical use was made by Apple to QuickType keyboard and Emoji suggestions by learning from millions of typing patterns without storing or identifying specific user interactions, using Differential Privacy. Also Google, in 2024 has achieved the largest known deployment of differential privacy, covering nearly three billion devices in products like Google Home, Android Search, and messages.